Numerical Integration

Numerical Integration#

Integration#

  • The integral of a function \(f(x)\) is evaluated using the fundamental theorem of calculus:

\[ \int\limits_a^b f(x)dx = F(b) - F(a) \]

  • Here, \(F(x)\) is the anti-derivative of \(f(x)\)

\[\frac{dF(x)}{dx} = f(x) \]

  • Functions for which exact integrals can be computed

\[\begin{split}\begin{aligned} &\begin{array}{c|c} \hline \hline f(x) & F(x)\\ \hline x^n (n\neq -1) & \frac{x^{n+1}}{n+1} \\ 1/x & ln(x) \\ e^x & e^x \\ sin(x) & -cos(x) \\ \hline \end{array} \end{aligned}\end{split}\]

  • Functions for which exact integrals cannot be computed

\[\begin{split}\begin{aligned} &\begin{array}{c|c} \hline e^{-x^2} & ? \\ x^x & ? \\ \hline \end{array} \end{aligned}\end{split}\]

Numerical Integration#

  • An intuitive understanding of an integral is:

\[ \int\limits_a^b f(x) dx = \text{net area under the curve} f(x) \]

  • Numerical integration methods approximate the area under the curve using simple geometrical shapes to evaluate definite integrals

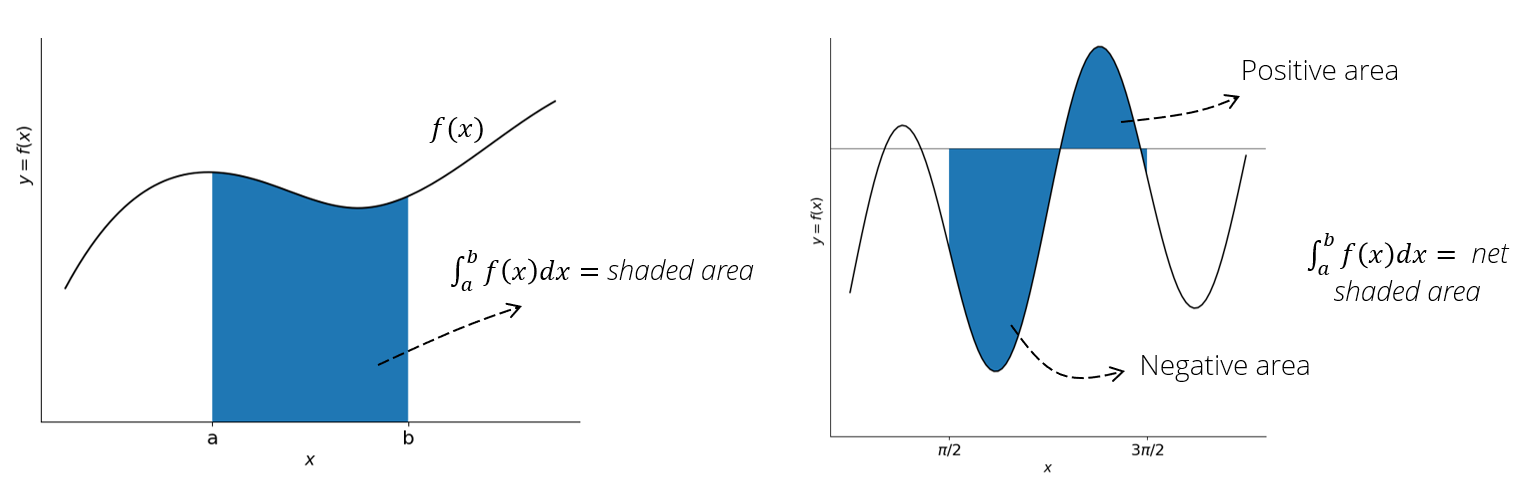
_images/integral.png

  • An integral can be approximed by summing the areas of a finite number of subdivisions

  • Numerical integration methods that use fixed samples of a function:

    • Reimann sums

    • Trapezoid rule

    • Simpson’s rule

  • These methods do not require the exact function definition

    • Useful for experimental data

  • Mathematically, these numercial methods divide the integration domain into sub-domains

  • The integral is then split into sum of integrals over each sub-domain

\[\begin{split} \begin{align*} \int\limits_a^b f(x) dx &= \sum_{i=0}^{n-1} \int\limits_{x_i}^{x_{i+1}} f(x) dx \\ &= \int\limits_{x_0 = a}^{x_{1}} f(x) dx + \int\limits_{x_1}^{x_{2}} f(x) dx + \cdots + \int\limits_{x_i}^{x_{i+1}} f(x) dx + \cdots + \int\limits_{x_{n-1}}^{x_{n}=b} f(x) dx \end{align*} \end{split}\]

  • Now, the Taylor series approximation of a function around \(x=x_p\)

\[ f(x) = f(x_p) + f^{(1)}(x_p) (x-x_p) + f^{(2)}(x_p) \frac{(x-x_p)^2}{2!} + \cdots \]

  • Substituting this into one of the integral (\(x_i \le x_p \le x_{i+1}\)):

\[ \int\limits_{x_i}^{x_{i+1}} f(x) dx = \int\limits_{x_i}^{x_{i+1}} \left(f(x_p) + f^{(1)}(x_p) (x-x_p) + f^{(2)}(x_p) \frac{(x-x_p)^2}{2!} + \cdots \right) dx \]

  • Integrating, we get (\(h = x_{i+1} - x_i\)):

\[ \int\limits_{x_i}^{x_{i+1}} f(x) dx = h f(x_p) + \frac{h}{2} (x_i + x_{i+1} - 2 x_p) f^{(1)}(x_p) + O(h^3) \]

Riemann Sums#

  • Riemann sums approximate the integrals using just the 1st term of the Taylor series

\[ \int\limits_{x_i}^{x_{i+1}} f(x) dx \approx h f(x_p) \]

  • In other words, Riemann sums assume the function is constant within a subdivision

    • The subdivision is rectangular in shape

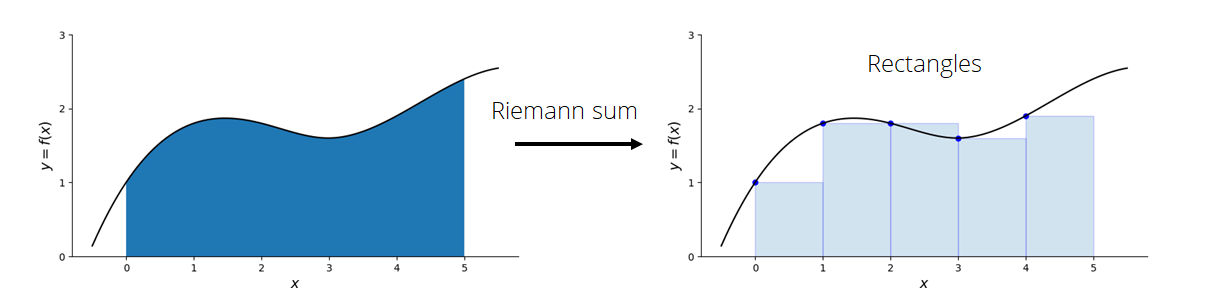
Riemann sum

  • Sum over the curve from \(a\) to \(b\) to approximate the definite integral

\[ \int_a^b f(x) \approx \sum A_i \]

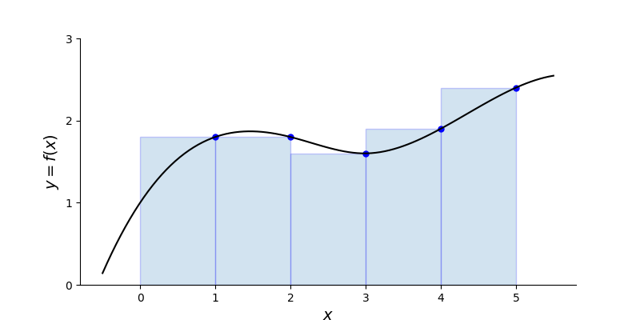
  • For left Riemann sum:

\[ A_i = h f(x_i) \]

  • Uses the left-most point of sub-domain \(x_i\) to compute the height of the rectangle

  • Right Riemann sum - uses the right-most point \(x_{i+1}\) to compute the height of the rectangle

\[ A_i = h f(x_{i+1}) \]
_images/rright.png

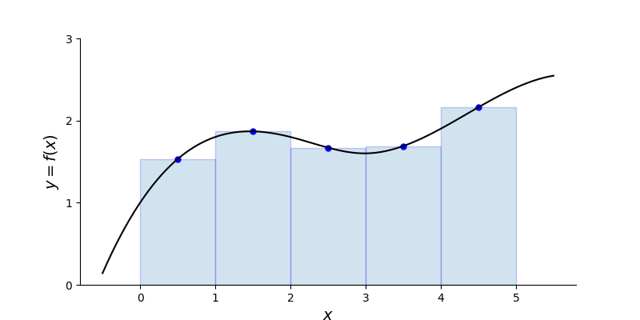
  • Midpoint Riemann sum - use the mid-point or equivalently, the average of the left and right points

\[ A_i = h f\left(\frac{x_i + x_{i+1}}{2}\right) \]
_images/rmid.png

Trapezoid Rule#

  • The trapezoid rule assumes that the function is linear within the sub-domain

    • The shape of the area under this linear approximation forms a trapezoid, hence the name

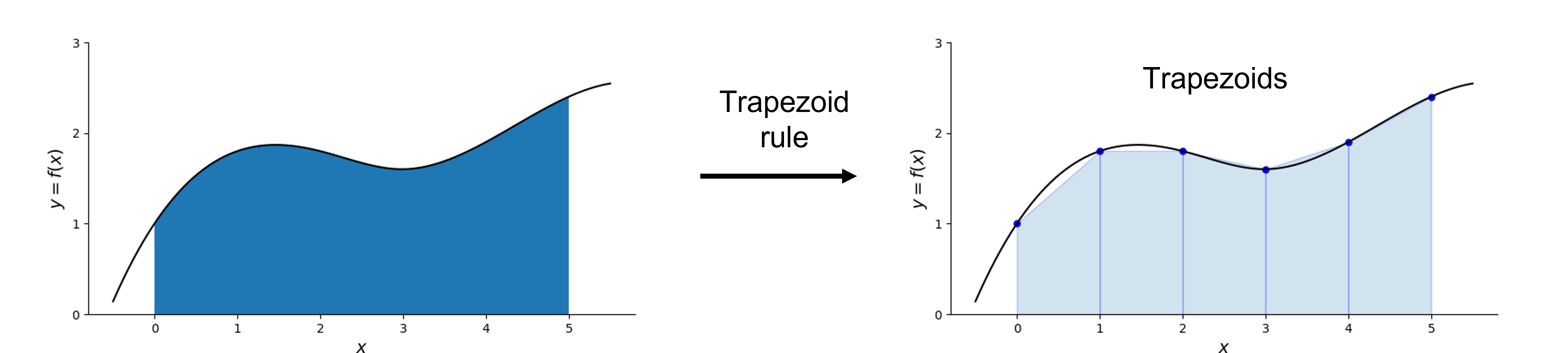
_images/trapz.png

  • The area for each subdivision is:

\[ A_i = \frac{h}{2}\Bigl( f(x_i) + f(x_{i+1}) \Bigr) \]

  • Trapezoidal integration is effectively the average of left and right Riemann sums

Simpson’s Rule#

  • Simpson’s rule uses a quadratic function to approximatge the function within a sub-domain consisting of 3 points

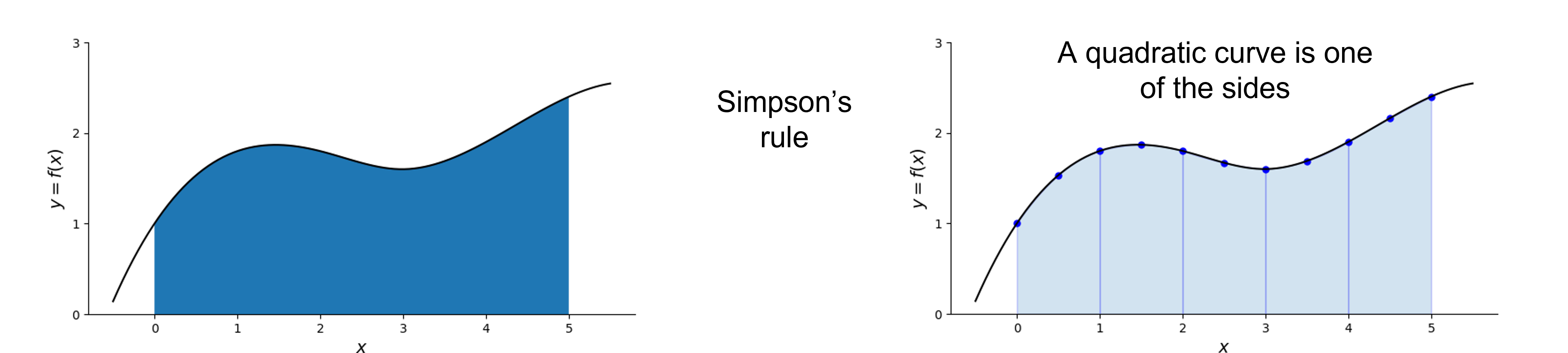
_images/simpsons.png _images/simpsons_gif.gif

Source: https://en.wikipedia.org/wiki/Simpson%27s_rule

  • According to Simpson’s rule:

\[ A_i = \frac{h}{3}\Bigl( f(x_{i}) +4f(x_{i+1/2}) + f(x_{i+1)} \Bigr) \]

Practical Considerations#

  • The error associated with:

    • left and right Reimann sums is \(O(h)\)

    • midpoint Reimann sums and trapezoidal rule is \(O(h^2)\)

    • Simpson’s rule is \(O(h^4)\)

  • Often, numerical integration is occuring on sampled experimental data

    • Thus, the step size is often controlled by the experimental conditions

    • Use of trapezoidal integration or Simpson’s rule is encouraged to reduce numerical errors

  • While the error associated with Simpson’s rule is small, it sometimes gives poor results with highly oscillatory functions

Interactive Demonstration#

%matplotlib widget

import numpy as np
from scipy import integrate, interpolate
import matplotlib.pyplot as plt

from ipywidgets import HBox, VBox, interactive, RadioButtons
from IPython.display import display

---------------------------------------------------------------------------
ModuleNotFoundError                       Traceback (most recent call last)
Cell In[1], line 1
----> 1 get_ipython().run_line_magic('matplotlib', 'widget')
      3 import numpy as np
      4 from scipy import integrate, interpolate

File /opt/hostedtoolcache/Python/3.11.9/x64/lib/python3.11/site-packages/IPython/core/interactiveshell.py:2480, in InteractiveShell.run_line_magic(self, magic_name, line, _stack_depth)
   2478     kwargs['local_ns'] = self.get_local_scope(stack_depth)
   2479 with self.builtin_trap:
-> 2480     result = fn(*args, **kwargs)
   2482 # The code below prevents the output from being displayed
   2483 # when using magics with decorator @output_can_be_silenced
   2484 # when the last Python token in the expression is a ';'.
   2485 if getattr(fn, magic.MAGIC_OUTPUT_CAN_BE_SILENCED, False):

File /opt/hostedtoolcache/Python/3.11.9/x64/lib/python3.11/site-packages/IPython/core/magics/pylab.py:103, in PylabMagics.matplotlib(self, line)
     98     print(
     99         "Available matplotlib backends: %s"
    100         % _list_matplotlib_backends_and_gui_loops()
    101     )
    102 else:
--> 103     gui, backend = self.shell.enable_matplotlib(args.gui.lower() if isinstance(args.gui, str) else args.gui)
    104     self._show_matplotlib_backend(args.gui, backend)

File /opt/hostedtoolcache/Python/3.11.9/x64/lib/python3.11/site-packages/IPython/core/interactiveshell.py:3665, in InteractiveShell.enable_matplotlib(self, gui)
   3662     import matplotlib_inline.backend_inline
   3664 from IPython.core import pylabtools as pt
-> 3665 gui, backend = pt.find_gui_and_backend(gui, self.pylab_gui_select)
   3667 if gui != None:
   3668     # If we have our first gui selection, store it
   3669     if self.pylab_gui_select is None:

File /opt/hostedtoolcache/Python/3.11.9/x64/lib/python3.11/site-packages/IPython/core/pylabtools.py:338, in find_gui_and_backend(gui, gui_select)
    321 def find_gui_and_backend(gui=None, gui_select=None):
    322     """Given a gui string return the gui and mpl backend.
    323 
    324     Parameters
   (...)
    335     'WXAgg','Qt4Agg','module://matplotlib_inline.backend_inline','agg').
    336     """
--> 338     import matplotlib
    340     if _matplotlib_manages_backends():
    341         backend_registry = matplotlib.backends.registry.backend_registry

ModuleNotFoundError: No module named 'matplotlib'

def numerical_int(f, a, b, N, method='Riemann'):
    '''Compute the Riemann sum of f(x) over the interval [a,b].

    Parameters
    ----------
    f : function -- Vectorized function of one variable
    a , b : float -- Endpoints of the interval [a,b]
    N : int -- Number of subintervals of equal length in the partition of [a,b]
    method : str -- Integration method; valid values 'Riemann', 'Trapezoid' or 'Simpsons'
        
    Returns
    -------
    float -- Approximation of the integral
    '''
    h = (b - a)/N
    x = np.linspace(a,b,N+1)

    if method == 'Riemann':
        x_mid = (x[:-1] + x[1:])/2
        return h*np.sum(f(x_mid))
    elif method == 'Trapezoid':
        return 0.5*h*np.sum(f(x[:-1]) + f(x[1:]))
    elif method == 'Simpsons':
        return (h/3)*np.sum(f(x[0:-1:2]) + 4*f(x[1::2]) + f(x[2::2]))
    else:
        raise ValueError("Method must be 'Riemann', 'Trapezoid' or 'Simpsons'.")

# Formatting stuff
fs = 20
ls = 20
lw = 2
ms = 10

# x values - global scope
x = np.linspace(-4, 4, 100)

# Radio button for choosing the function
funcButton = RadioButtons(options=['Quadratic'], 
                       value='Quadratic', 
                       layout={'width': 'max-content'}, # If the items' names are long
                       description='Integrand', disabled=False)

fig, ax = plt.subplots(figsize=(10, 10))

# Interactive plot function callback
def plot_func(IntMeth, Function, N=2):
    # Clear figure
    ax.clear()

    # Set function
    f = None
    fIntExact = None
    titleText = None
    if Function == 'Quadratic':
        f = lambda x: 5 - 0.25*x**2
        fIntExact = 56/3
        titleText = r"$(5 - 0.25x^2)$"
    elif Function == 'Cubic':
        f = lambda x: 5 - 0.1*x**3
        fIntExact = 20
        titleText = r"$(5 - 0.1x^3)$"
    elif Function == 'Quartic':
        f = lambda x: 5 - 0.025*x**4
        fIntExact = 19.68
        titleText = r"$(5 - 0.025x^4)$"
    elif Function == 'Exponential':
        f = lambda x: np.exp(0.1*x)
        fIntExact = 20*np.sinh(0.2)
        titleText = r"$e^{0.1x}$"
    elif Function == 'Cos':
        f = lambda x: np.cos(1.4*np.pi*x)
        fIntExact = np.sin(2.8*np.pi)/0.7/np.pi
        titleText = r"$cos(1.4 \pi x)$"

    # Integration bounds
    a = -2
    b = 2

    # Numerical integrated value
    fInt = numerical_int(f, a, b, N, IntMeth)
    err = (fInt/fIntExact - 1)*100
    ax.set_title(r"$\int_a^b $" + titleText + r"$ dx \approx $" + f"{fInt:4.4f}\nError = {err:4.2f}%\n", fontsize=fs)

    # Line plot of the function
    ax.plot(x, f(x), 'black', lw=lw)
    ax.set_xlabel('$\it{x}$', fontsize=fs)
    ax.set_ylabel('$f(x)$', fontsize=fs)
    #ax.set_xlim(0,6)
    #ax.set_ylim(-1, 110)
    ax.tick_params(axis='both', labelsize=ls)

    # Geometry used for integration
    xSam = np.linspace(-2, 2, N+1)
    if IntMeth == 'Riemann':
        x_mid = (xSam[:-1] + xSam[1:])/2 # Midpoints
        y_mid = f(x_mid)
        ax.plot(x_mid, y_mid, 'b.', markersize=ms)
        ax.bar(x_mid, y_mid, width=4/N, alpha=0.2, edgecolor='b', color='tab:blue')
    elif IntMeth == 'Trapezoid':
        for i in range(N):
            x0 = xSam[i]
            x1 = xSam[i + 1]
            ax.plot(xSam, f(xSam), 'b.', markersize=ms)
            ax.fill_between([x0, x1],[f(x0), f(x1)], color='tab:blue', alpha=0.2, edgecolor='b')
    else:
        for i in range(N//2):
            x0 = xSam[2*i]
            x1 = xSam[2*i + 2]
            xm = xSam[2*i + 1]
            [y0, ym, y1] = [f(x0), f(xm), f(x1)]
            xp = np.linspace(x0, x1, 20)
            h = xm-x0
            yp = (y0/(2*h**2))*(xp-xm)*(xp-x1) \
               - (ym/(  h**2))*(xp-x0)*(xp-x1) \
               + (y1/(2*h**2))*(xp-xm)*(xp-x0)
            ax.plot(xSam, f(xSam), 'b.', markersize=ms)
            ax.fill_between(xp, yp, color='tab:blue', alpha=0.2, edgecolor='b')

    fig.canvas.draw_idle()
    #fig.canvas.flush_events()
    plt.show()

interactive_plot = interactive(plot_func, N=(2, 16, 2), 
                                          IntMeth=['Riemann', 'Trapezoid', 'Simpsons'],
                                          Function=['Quadratic', 'Cubic', 'Quartic', 'Exponential', 'Cos'])
output = interactive_plot.children[-1]
output.layout.height = '1200px'

#buttons.observe(updateF, names='value')
display(interactive_plot)

Gauss Integration#

  • Provides numerical integration rules specialized for polynomials

  • Also known as Gausian quadrature

    • \(w_{in} = \) integration weights

    • \(\zeta_{in} = \) integration points

    • \(n = \) number of Gauss integration points \((\geq 1)\)

\[ \int\limits_{-1}^1 f(\zeta)d\zeta \approx \sum_{i=1}^2 w_{in}f(\zeta_{in}) \]

  • It can be shown that with \(n\) integration points, choosing the integration points to be the roots of the degree-\(n\) Legendre polynomial, \(P_n(x)\) gives exact results for polynomials of order \(2n-1\) (Gauss-Legendre quadrature)

Integrating with scipy.integrate#

  • The integrate sub-module of scipy provides various functions for numerical integration

    • Integration using samples

      • trapezoid - same as trapz from numpy

      • simpson

      • cumulative_trapezoid - returns a numpy array with integral evaluated as a function of x

    • Integration when a function object is available

      • fixed_quad - integration using Gaussian quadrature

      • quad - integration using adaptinve quadrature methods

      • dblquad, tplquad - double and triple integration

      • nquad - higher order integration with arbitrary number of variables

  • Example: evaluate \( \int\limits_o^\pi sin(x) dx \)

from scipy import integrate

# 20 samples of sin(x)
x = np.linspace(0, np.pi, 20)
y = np.sin(x)

# Exact solution 
int_exact = -np.cos(np.pi) + np.cos(0)

# numerical integration
int_t = integrate.trapezoid(y, x)
int_s = integrate.simpson(y, x)

print(f'{"Exact: ":>16}{int_exact}\n{"Trapezoid Rule: ":>16}{int_t}\n{"Simpson`s Rule: ":>16}{int_s}')

  • If \(f(x)\) is the input, then cumulative_trapezoid function computes samples of the integrated function

\[g(x) = \int\limits_a^x f(x) dx\]

  • Example:

\[f(x) = sin(x)\]
\[\Rightarrow g(x) = cos(a) - cos(x)\]
x = np.linspace(0, np.pi, 20)
y = np.sin(x)

# Cumulative integration with initial value (a) = 0
y_int = integrate.cumulative_trapezoid(y, x, initial=0)

# For plotting exact value
x_e = np.linspace(0, np.pi, 200)
y_e = np.sin(x_e)
y_int_e = 1 - np.cos(x_e)

# Plot
fig, ax = plt.subplots()
ax.plot(x_e, y_e, '-k', label='sin(x)')
ax.plot(x_e, y_int_e, '-r', label='$\int_0^x sin(x)dx = 1-cos(x)$')
ax.plot(x, y_int,'or', markersize=3, label='Cum. Trapezoid')
ax.set_xlabel('x')
ax.legend();

Scipy Integration#

  • Integration given function objects

    • quad, fixed_quad, dblquad, tplquad, nquad

  • Example: evaluate \(\int\limits_0^{\pi} sin(x) dx\)

    • The exact value is 2

def f(x):
    return np.sin(x)

integrate.fixed_quad(f, 0, np.pi, n=5)

(2.0000001102844727, None)

  • The first value in the output tuple is the integral

  • The second value is alway None

# Adaptive Gauss-Kronrod quadrature
integrate.quad(f, 0, np.pi)

(2.0, 2.220446049250313e-14)

  • The first value in the output tuple is the integral

  • The second value is the estimated error

  • Example: evaluate \(\int\limits_0^\infty e^{-x^2} dx\)

  • Mathemeticians have defined a special function called the error function because this integral appear fairly commonly:

\[ erf(x) = \frac{2}{\sqrt{\pi}} \int_0^x e^{-x^2} dx\]
def f(x):
    return np.exp(-x**2)

# Using Gauss quadrature
val = integrate.quad(f, 0, np.inf)
print(val[0])

0.8862269254527579

from scipy.special import erf

# using the error function
val2 = np.sqrt(np.pi)/2*erf(np.inf)
print(val2)

0.8862269254527579

Reference Material#

Contents