Scipy

Scipy#

  • Scipy, pronounced sigh pie, is a Python library (a set of modules) for scientific computing

  • Builds on numpy; numpy is like Matlab and scipy modules are the toolboxes

  • Provides specialized sub-modules with algorithms for:

  • Linear algebra – scipy.linalg

    • More advanced and efficient than numpy.linalg

  • Sparse linear algebra – scipy.sparse.linalg

    • Linear algebra with sparse matrices (matrices with mostly zeros as elements)

  • Interpolation – scipy.interpolate

  • Optimization – scipy.optimize

  • Statistics – scipy.stats

  • Numerical integration – scipy.integrate

  • Signal processing – scipy.signal

  • Special mathematical functions like Bessel functions, - Elliptic functions– scipy.special

  • Mathematical and physical constants – scipy.constants

Tips for Scipy and Beyond#

  • There is not nearly enough time to discuss every function/package/library

  • If you want to do something specific, there is probably a package/function for it

    • Graphics and visualization - VTK, PyVista, PyMol, VPython, …

    • User interfaces - PyQt5, Tkinter, Kivy, wxPython, …

    • Plotting - matplotlib, plotly, bokeh, seaborn, …

    • Material properties - CoolProp

    • CAD - CADQuery

    • Finite element analysis - SfePy, Fenics, NGSolve, …

    • Machine learning - TensorFlow, PyTorch, scikit-learn, …

    • …

  • Learning how to find useful packages and use them is an invaluable skill

  • The less you have to do manually, the better

Linear Algebra Example#

  • Linear system of equations frequently appear in engineering and adjacent fields

    \[\begin{split} \begin{array}{cccc} x_1 &+& 3x_2 &+& 5x_3 &=& 10 \\ 2x_1 &+& 5x_2 &+& x_3 &=& 8 \\ 2x_1 &+& 3x_2 &+& 8x_3 &=& 3 \end{array} \end{split}\]
🠓 Matrix Form
\[\begin{split} \begin{matrix} \begin{pmatrix} 1 & 3 & 5 \\ 2 & 5 & 1 \\ 2 & 3 & 8 \end{pmatrix} \\ A \end{matrix} \begin{matrix} \begin{pmatrix} x_1 \\ x_2 \\ x_3 \end{pmatrix} \\ x \end{matrix} = \begin{matrix} \begin{pmatrix} 10 \\ 8 \\ 3 \end{pmatrix} \\ b \end{matrix} \end{split}\]
\[\begin{split} Ax=b \implies x=A^{-1}b = \begin{pmatrix} -9.28 \\ 5.16 \\ 0.76 \end{pmatrix} \end{split}\]
import numpy as np
from scipy import linalg

---------------------------------------------------------------------------
ModuleNotFoundError                       Traceback (most recent call last)
Cell In[1], line 1
----> 1 import numpy as np
      2 from scipy import linalg

ModuleNotFoundError: No module named 'numpy'

A = np.array([[1, 3, 5],
              [2, 5, 1],
              [2, 3, 8]])
b = np.array([10, 8, 3])

%timeit A_inv = linalg.inv(A); x1 = A_inv@b

7.54 µs ± 30.7 ns per loop (mean ± std. dev. of 7 runs, 100,000 loops each)

%timeit x2 = linalg.solve(A, b)

11.1 µs ± 45.9 ns per loop (mean ± std. dev. of 7 runs, 100,000 loops each)

  • Explicitly computing the inverse is expensive

  • The linalg.solve function uses a more efficient algorithm and should be favored

Optimization Example#

  • Engineering problems often involve optimization of complicated functions of several vairables

    • Use the optimize.minimize function

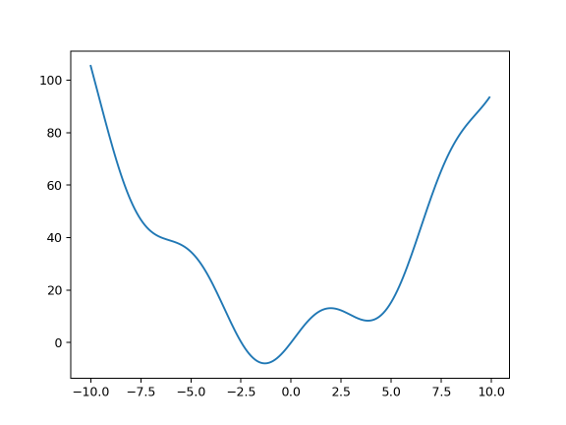
_images/optimize.png 
from scipy import optimize

# Function to be optimized
def f(x):
    return x**2 + 10*np.sin(x)

# Optimize w/ initial guess of 0
optimize.minimize(f, x0=0.)

  message: Optimization terminated successfully.
  success: True
   status: 0
      fun: -7.945823375615206
        x: [-1.306e+00]
      nit: 5
      jac: [-1.192e-06]
 hess_inv: [[ 8.589e-02]]
     nfev: 12
     njev: 6

Scientific Computing#

  • Physical phenomena can be modelled mathematically

  • In many cases, these mathematical models take the form of differential equations

    • Less commonly, they take the form of integral equations or integro-differential equations

  • Numerical methods convert these idealized mathematical models into a linear system of equations

  • The linear systems of equations are solved using linear algebra packages

  • Examples of commonly used numerical methods:

    • Finite difference method (FDM)

    • Finite element method (FEM)

    • Finite volume method (FVM)

    • Molecular dynamics (MD)

    • Density functional theory (DFT)

    • …

  • High-level programming languages like Matlab and Python (via scipy) provide an interface to the linear algebra packages written in C or Fortran

  • Engineering design problems require a physical quantity (e.g., weight, cost, stiffness) to be optimized given specific constraints on other physical quantities (e.g., weight, max stress)

    • Optimization procedures from libraries such as scipy.optimize or Matlab are used to solve such design problems

  • In some engineering scenarios, experiments are used to build a mathematical model from noisy data

    • Statistics and interpolation (a specific kind of optimization) are employed

    • scipy.interpolate and scipy.statistics provide interpolation algorithms and statistical functions, respectively

    • R, Matlab/Octave and Julia provide alternate options

  • Step-by-step approach to devising a numerical model

    • Understand

      • the physics

      • the parameters (e.g., material properties, geometry), and

      • the observables (e.g., temperature, displacements, velocities)

    • Identify or develop the mathematical model of the physical phenomenon

      • E.g., Newton’s law, Schrodinger’s equation, Navier-Stokes equations, Maxwell’s equations

      • Create simplifying assumptions

    • Synthesize a computational model using various programming concepts and libraries such as numpy, scipy, as necessary

    • Verify the model for correctness

Correctness of a Computational Model#

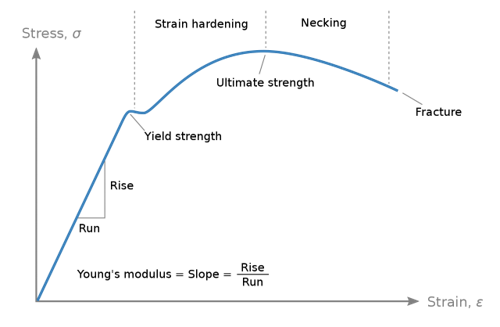
  • Phenomenologically correct

    • Example: materials are assumed to have a linear response to an applied strain – generalized Hooke’s law

    • This assumption holds true for small strains and breaks down at finite strains

_images/stress.png

  • Methodologically correct

    • Example: numerical approximation of the derivative of a function 𝑓(𝑥):
      \(\frac{df(x)}{dx}\approx \frac{f(x+h) - f(x)}{h}\)

      • ℎ cannot be too small or too large

      • 𝑓 should be a well-behaved function

      • If neither of these conditions are met, the approximate derivative will not be correct affecting the whole computational model

  • Numerically correct

    • Example: numerical errors due to finite precision of floating-point numbers

3*0.1 == 0.3

3*0.1

  • A robust approach is needed to get around such issues

3*0.1 - 0.3 < 1e-8

Sympy#

  • Stands for symbolic Python

  • Allows for symbolic equation manipulation

  • Useful for solving symbolically:

    • Systems of equations

    • Integrals and Derivatives

    • Limits

    • Differential equations

  • Symbolic variables must be defined with the symbols function

  • Equations are defined with the Eq function

  • Equations and systems can be solved with the solve function

  • Example: system of equations

\(x+y = 5\)

\(x = y - 3\)

import sympy as sp

x, y = sp.symbols('x y') # commas or spaces can be used

eqn1 = sp.Eq(x + y, 5)
eqn2 = sp.Eq(x, y - 3)

sol = sp.solve([eqn1, eqn2], [x, y])
print(sol)

{x: 1, y: 4}

  • Example: multiple solutions

\(x+y = 5\)

\(x^2 + y^2 = 17\)

eqn2 = sp.Eq(x**2 + y**2, 17)
sol = sp.solve([eqn1, eqn2],[x, y])
print(sol)

[(1, 4), (4, 1)]

  • Example: statics problem

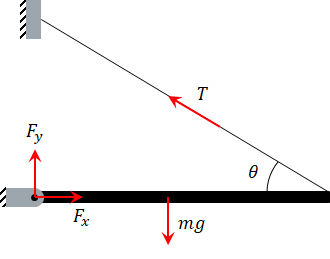
_images/example_statics_problem.png 
Fx, Fy, T = sp.symbols('F_x, F_y, T')
mg, th = sp.symbols('mg, theta')

# Fx - cos(th) T = 0
eq1 = sp.Eq(Fx - sp.cos(th)*T, 0)

# Fy + sin(th) T = mg
eq2 = sp.Eq(Fy + sp.sin(th)*T, mg)

# sin(th) T = mg/2
eq3 = sp.Eq(2*sp.sin(th)*T, mg)

sol = sp.solve([eq1, eq2, eq3], [Fx, Fy, T])
print(sol)

{F_x: mg*cos(theta)/(2*sin(theta)), F_y: mg/2, T: mg/(2*sin(theta))}

from IPython.display import display, Math

for item in sol.items():
    display(Math(sp.latex(item[0]) + " = " + \
            sp.latex(sp.simplify(item[1]))))        # Formats the ouput using LaTex (or its web versions KaTex in VS Code and MathJax in a browser) - a typesetting system
\[\displaystyle F_{x} = \frac{mg}{2 \tan{\left(\theta \right)}}\]
\[\displaystyle F_{y} = \frac{mg}{2}\]
\[\displaystyle T = \frac{mg}{2 \sin{\left(\theta \right)}}\]

  • sp.simplify - simplifies the symbolic expression

for item in sol.items():
    num_val = item[1].subs(((mg, 1000), (th, np.pi/6))) # Input is a dictionary or a sequence
    print(f"{item[0]} = {num_val:.2f}")

F_x = 866.03
F_y = 500.00
T = 1000.00

  • var.subs method takes a dictionary or sequence of 2-tuples as input and substitutes the symbols with numeric values

  • var.evalf method numerically evaluates symbolic expressions

Integration and Differentiation in Sympy#

  • Use the diff and integrate functions

    • diff can also perform partial derivatives

expr = y*x**2 + x*y**y + 1
expr
\[\displaystyle x^{2} y + x y^{y} + 1\]
x_diff = sp.diff(expr, x)
x_diff
\[\displaystyle 2 x y + y^{y}\]
y_diff = sp.diff(expr, y)
y_diff
\[\displaystyle x^{2} + x y^{y} \left(\log{\left(y \right)} + 1\right)\]
x_int = sp.integrate(expr, x)
x_int
\[\displaystyle \frac{x^{3} y}{3} + \frac{x^{2} y^{y}}{2} + x\]
Contents